Spacetime Physics, Chapter 7

The combination of the motion descriptive quantities (momentum and energy) of two colliding bodies is conserved. We call this combined quantity momentum-energy or momenergy.

7.2 Momenergy Arrow

Magnitude of a particle’s momenergy is its mass. Momenergy is a directed quantity.

Momenergy is a 4-vector: Momenergy is 4-dimensional vector in spacetime:

Particle momenergy points along the particle’s worldline in spacetime. It points in the direction of particle’s spacetime displacement.

Momenergy exists independently of reference frames. Particle wristwatch measures proper time for that displacement.

The resulting expression is:

$$ (\text{momenergy}) = (\text{mass}) \times \frac{(\text{spacetime displacement})}{(\text{proper time for that displacement})} $$

The unit 4-vector (spacetime displacement / proper time) defines and measures the direction of the worldline displacement, and therefore the direction of the momenergy 4-vector.

Law of Momenergy Conservation: Total momenergy before reaction = total momenergy after reaction.

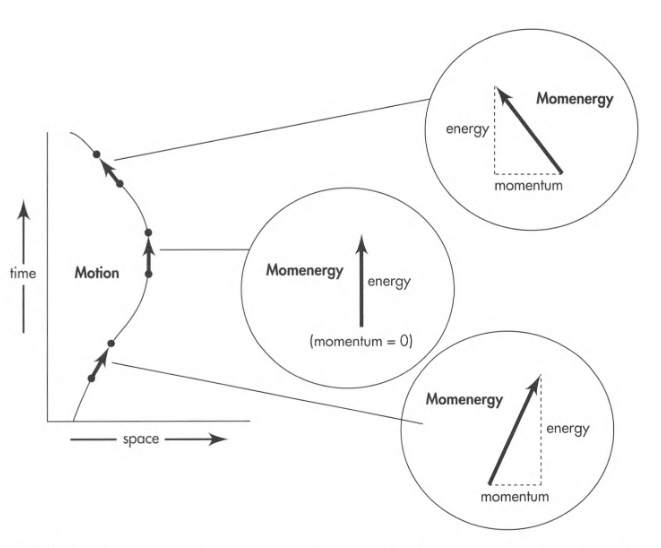
Since we measure time and space using the same units, momenergy has the same unit as the first factor: mass. This means we measure momentum and energy using the same unit: mass.

7.3 Momenergy Components and Magnitude

Spacetime location of an event unites time and space. Similarly, the single idea of momenergy unites momentum and energy.

When we choose a reference frame,

The calculus version of this is:

$$ \begin{aligned} E &= m \frac{dt}{d\tau} \\[0.5em] p_x &= m \frac{dx}{d\tau} \\[0.5em] p_y &= m \frac{dy}{d\tau} \\[0.5em] p_z &= m \frac{dz}{d\tau} \end{aligned} $$

Then we have:

$$ \begin{aligned} (\text{magnitude }&\text{of momenergy arrow})^2 \\[0.7em] \quad &= E^2 - p^2 \\[0.5em] \quad &= E^2 - p_x^2 - p_y^2 - p_z^2 \\[0.5em] \quad &= m^2 \left( \frac{dt^2 - dx^2 - dy^2 - dz^2}{d\tau^2} \right) \\[0.5em] \quad &= m^2 \left( \frac{d\tau^2}{d\tau^2} \right) \\[0.5em] \quad &= m^2 \end{aligned} $$

Since mass of a particle is invariant and we have $m^2 = E^2 - p^2$, then assuming $p_y = p_z = 0$, the momenergy 4-vector for a single vector as observed from different frames form a hyperbola in the energy-momentum plane:

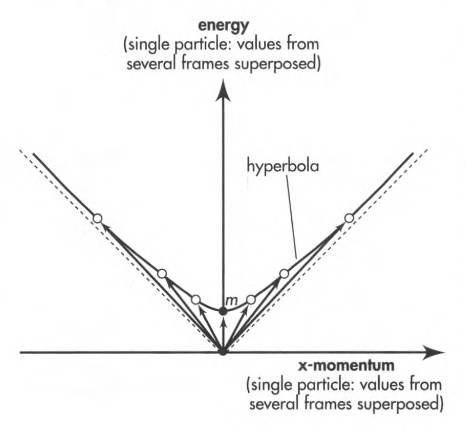
Length of these arrows in the Lorentz geometry is invariant: always equal to the mass of the particle.

Momenergy 4-vector of a material particle is always timelike. It always lies in the same spacetime direction as the particle’s worldline. The events along the worldline have a timelike relation: Time separation exceeds space separation.

7.4 Momentum: “Space Part” of Momenergy

Newton called momentum “quantity of motion”. In Newtonian physics, we have $p = m \dfrac{ds}{dt}$ (valid for low velocities).

Assume a particle moves with speed $v$ in the $x$ direction. Then $x = vt$, and therefore $dx = v dt$.

Then we have:

$$ \begin{aligned} d\tau &= [(d\tau)^2]^{1/2} = [(dt)^2 - (dx)^2]^{1/2} = [(dt)^2 - (v dt)^2]^{1/2} \\[0.5em] &= (dt) (1 - v^2)^{1/2} = \frac{dt}{\gamma} \end{aligned} $$

So, the proper time between two nearby events is always less than the lab time.

Then:

$$ \begin{aligned} E = m \frac{dt}{d\tau} &= m \gamma \\[0.5em] p_x = m \frac{dx}{d\tau} &= m v_x \gamma \end{aligned} $$

The momentum expression is the same as in Newtonian physics, except for the factor $\gamma$. That factor is close to 1 for low speeds.

But as speed approaches the speed of light, the particle acquires a momentum much greater than the Newtonian value.

Relativistic expression for momentum is:

$$ p = m v \gamma = \frac{m v}{\sqrt{1 - v^2}} \tag{7.8} $$

7.5 Energy: “Time Part” of Momenergy

As measured in a particular free-float frame, time component of momenergy is

$$ E = m \dfrac{dt}{d\tau} = m \gamma $$

Compare this with the Newtonian kinetic energy expression

$$ K_{\text{Newton}} = \frac{1}{2} m v^2 $$

At zero speed, the relativistic energy becomes equal to mass:

$$ E_{\text{rest}} = m $$

This is the rest energy of the particle.

In Newtonian mechanics, any constant can be added to the energy of a particle without changing the laws that describe motion.

This leads us to define kinetic energy as energy above rest energy:

$$ (\text{energy}) = (\text{rest energy}) + (\text{kinetic energy}) $$

or

$$ E = m + K $$

Thus, relativistic expression for kinetic energy is:

$$ K = m (\gamma - 1) = m \left( \frac{1}{\sqrt{1 - v^2}} - 1 \right) \tag{7.15} $$

Dividing momentum (7.10) by kinetic energy (7.15):

$$ v = \frac{p}{E} \tag{7.16} $$

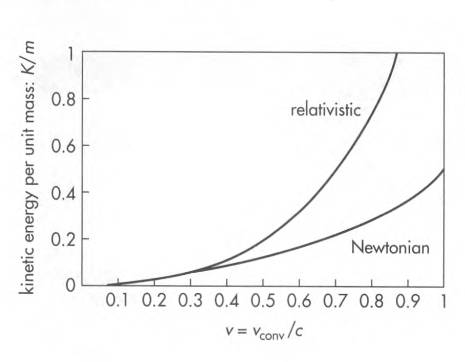
In figure below, we see kinetic energy as a function of speed, as predicted by relativistic (valid for any speed) and Newtonian (valid for low speeds) mechanics.

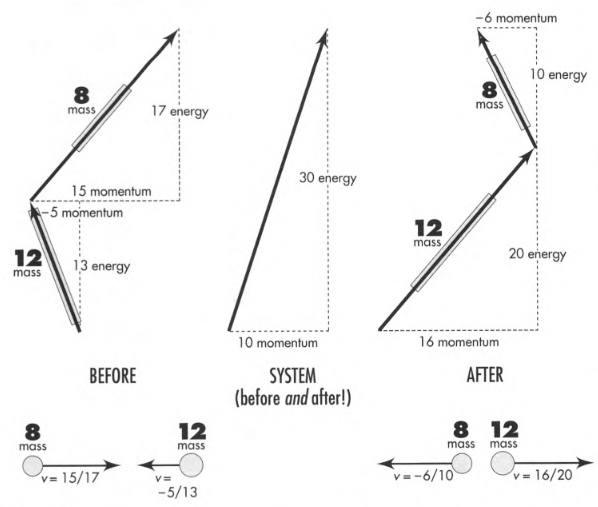
7.6 Conservation of Momenergy and its Consequences

Each component of momenergy is conserved in any interaction. That means:

Summary

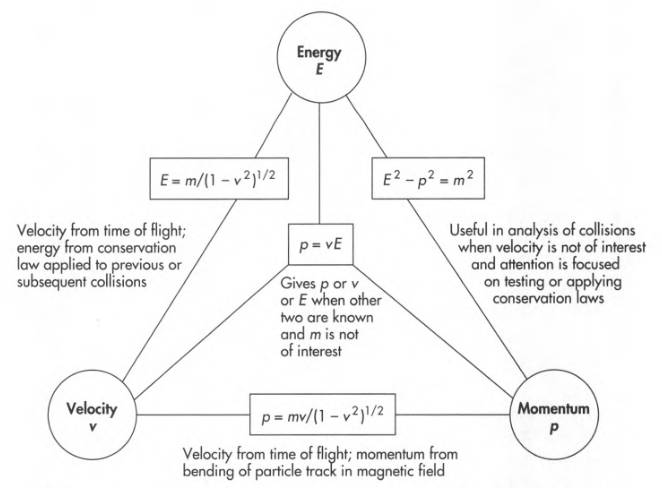
Formulas that relate momentum, energy, mass, and velocity of a particle: